Temperature is one of the important factors affecting MEMS gyroscope, which will greatly affect the output of MEMS gyro. MEMS gyroscope belongs to the temperature sensitive period, and its material is semiconductor silicon. When the temperature changes, the thermal expansion coefficient, elastic modulus, and resonant frequency of the silicon wafer will change, which will affect the performance of the MEMS gyroscopes, mainly bias. Based on MEMS, the most temperature-dependent factors belong to the field of oil logging and drilling while, because of the harsh working environment in this field, downhole high temperature and other conditions, the accuracy of MEMS gyroscopes will be more affected. Therefore, it is very important to take compensation measures. The following will introduce common temperature compensation methods, temperature characteristic model analysis, application of Markov chain in MEMS gyro and temperature zero deviation compensation experiment.
Common MEMS gyro temperature compensation method
In order to make the accuracy of MEMS gyros not affected, we must take a method to compensate it. Currently, there are two commonly used methods: one is to install a constant temperature device outside the MEMS gyros, through the control circuit, so that the MEMS gyroscope works at a stable temperature, but it will make the system complicated and the volume becomes larger, and it is difficult to apply in the downhole drilling system; The second is to establish a temperature compensation model to compensate the output of MEMS gyro through software algorithm to reduce the error. Compared with the first method, this method is simpler to implement and less affected by the environment, and can achieve higher accuracy under the same hardware conditions. The common compensation algorithms include polynomial fitting, piecewise fitting and gray theory model compensation. The characteristics and comparison of these algorithms are shown in Table 1.
| Algorithm | Characteristic | Defect |
| Polynomial fitting method | For polynomial fitting of the gyro output characteristics in the full temperature region, the fitting coefficients are obtained by least squares and brought into the model for solution. | It is not suitable for irregular non-linear changes in the temperature curve. There is over-fitting phenomenon and the compensation generalization error is large. |
| Segmental fitting | The average temperature is divided into equidistant intervals, and polynomial fitting is carried out respectively | When the interval is small, the fitting is not accurate. When the interval is too long, the fitting parameters are too many and the precision is not high |
| Gray theory model compensation method | Taking the original zero deviation as the standard, the zero deviation of gyroscope at different temperatures is correlated, and the variation rule is found out and solved by differential equation | The correlation is not accurate and the error accumulation is obvious |
Table 1 Comparison of common temperature compensation algorithms
The above temperature bias compensation algorithms are more and more effective programs at present, but they all have more or less defects and need to be further improved. Based on the temperature characteristic model of MEMS gyros, a temperature compensation algorithm based on Markov process is proposed and compared with other algorithms.
Analysis of temperature characteristic model of MEMS gyroscope
Temperature variation has a great influence on the output of MEMS gyro sensor, so the temperature characteristic experiment of MEMS gyroscopes is usually carried out first, and then how the temperature variation affects the bias of the gyroscope is determined by the experimental data. The most commonly used method of bias characteristic of gyro temperature is polynomial fitting method. Among them, the polynomial established according to the relationship between the gyro output and temperature is:
F(x)=αmxm+...+α1x+α0
Where x represents the temperature of the gyroscope, αm,...,α1,α0 represents the coefficient of the gyro-zero partial fitting polynomial model, and represents the order of the polynomial. It can be seen that the polynomial of the relation between the gyro output and temperature is nonlinear and multivariate, which needs linearization and the coefficient of the model is obtained by least square method. The multivariate nonlinear to linear transformation is as follows.
Polynomials with known multivariate nonlinearity are:
![]()
When:
![]()
Then the multivariate nonlinear polynomial is:
![]()
The above formula is a linear multivariate equation. When the data has z groups, the linear relationship is:
F1(x)=α0+α1y11+α2y21+α3y31+...+αmym1+σ1
...
Fz(x)=α0+α1y1z+α2y2z+α3y3z+...+αmymz+σz
The matrix form of the above formula is:
F(x)=aY
Among them:
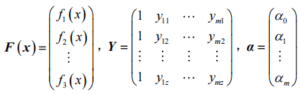
The least square fitting coefficient is:
α=(YTY)-1YTF(x)
The fitting coefficient of the above formula is put into the polynomial established according to the relationship between gyro output and temperature, then the MEMS gyros temperature bias error model can be obtained, and the error can be compensated within the allowable range of temperature.
Application of Markov chain in MEMS gyro bias compensation
A Markov chain is a random process, discrete in time, that transitions from one state to another. Markov chains are "memory-free" random processes in which the probability of the next state is determined only by the current state, regardless of the earlier time. The Markov process is controllable, and the system chooses to transfer the state or leave the current state unchanged according to probability. The process of moving from a point in the state diagram to the state of an adjacent point in a Markov process is called a random walk, and the adjacent points can be transformed at will with the same probability. A Markov chain is defined as a random sequence in a discrete space {M(x)|x=0,1,2... }, at any time y satisfies:
P[M(xy+k)]=j|M(x1)=i1,M(x2)=i2,...,M(xy)=iy]
=P[M(xy+k)=j|M(xy)=iy]
Then this sequence is a Markov chain. Where, i1,i2,... in,j represents the state at any time.
The MEMS gyro sensor output can be viewed as a closed-loop system, so the MEMS gyros can be associated with a Markov chain, described as:
M(tn)=AM(tn-1)+BU(tn-1)+e
Among them, M(tn) and M(tn-1) represent the output of the gyroscope, U(tn-1) is the factor affecting the output of the MEMS gyroscope, and e represents random noise. Generally, measures are taken to control the gyroscope, which can be ignored. A and B represent matrix dimensions. According to the Markov process output is not affected by the output before and after, where the probability M(tn+k)-M(tn) distribution is related to tn+ k-tk. Therefore, the temperature compensation model of MEMS gyroscopes can be described through the time-Markov process, and the model is:
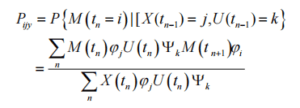
In the formula, Ψk, Φi, Φj respectively represent the probability density function of the Kth control quantity, and the probability density function in the state of i and j.
In engineering, random number algorithm is often used to solve the probability problem of a certain temperature, and the average temperature is taken as the final value through random sampling, that is, the desired solution.
In the MEMS gyros temperature drift output system, the number of state quantity and control quantity are selected as m and n respectively, then Pijy is the transfer probability of nmm latitude. Sampling the temperature model, the next state value is determined by random number algorithm, and the system input and output Markov state is:
j=argmin|m(t)-Mj
k=argmin|u(t)-Uk
In the formula, m(t), u(t) are the input data, Mj, Uk are the center point of the interval. Calculate j, k can get P, and then get each transition probability. The next state is calculated as follows:
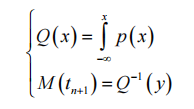
By calculating Q(x) and Q(y), the fitting curve of Markov chain can be obtained. After fitting is completed, the output value after error compensation can be obtained by bringing it into the temperature compensation model.
Temperature bias compensation experiment of MEMS gyroscope
In order to verify that the Markov chain proposed in the above section has a certain effect on the temperature compensation of MEMS gyro, the temperature zero deviation experiment of MEMS gyro is set up in this section. The MEMS gyro sensor was placed in a high and low temperature box in the laboratory with a collection frequency of 100 Hz. The X-axis was used as the experimental axis to collect and record the zero deviation of temperature and X-axis output. Specific experimental steps are as follows:
1. Place the MEMS gyrosensor in a high and low temperature box and preheat it with electricity at room temperature.
2. After the end of preheating, the advanced cooling, through the temperature box set the temperature to -10℃, after the temperature reaches, stop cooling and heat preservation for 1 hour
3. Start the heating experiment, set the temperature at 50℃, and slowly heat up through the temperature box. After reaching the temperature, keep the temperature for 1 hour, record the temperature while heating up, collect the output data of MEMS gyros, and save it.
4. Start the cooling experiment, set the temperature to -10℃, and slowly cool down through the temperature box. After reaching the temperature, keep it warm for 1 hour, record the temperature while cooling, collect the output data of MEMS gyroscopes,and save it.
5. Stop recording data. When the temperature drops to room temperature, power off the MEMS gyroscope.
6. Conduct repeated experiments and take average values.
The original zero-bias data of MEMS gyro output in the above temperature experiment is drawn in Matlab, as shown in Figure 1.
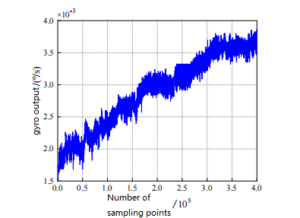
Figure 1 Original zero-bias data of MEMS gyro
The fitting curve of the Markov chain model is compared with the output of the gyroscope compensated by the Markov chain model, as shown in Figure 2. Blue represents the original output of the Markov chain model, and orange represents the output after the compensation of the Markov chain model.
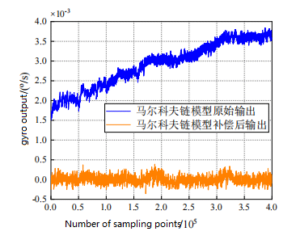
Figure 2 Comparison of Markov chain model before and after temperature compensation
It can be seen from Figure 1 and Figure 2 that the original output curve of Markov chain model and the original data output curve of MEMS gyroscopes are consistent and relatively fit. After compensation, the output curve of MEMS gyroscope becomes stable, and the variation amplitude is stable around 0. In order to further reflect the effect of Markov chain model compensation, the output of MEMS gyro sensor is compensated by polynomial fitting and piecewise fitting respectively. The compensation outputs of the three methods are plotted respectively, as shown in Figure 3, 4, and 5.
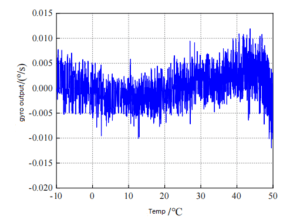
Figure 3 Polynomial fitting compensation curve
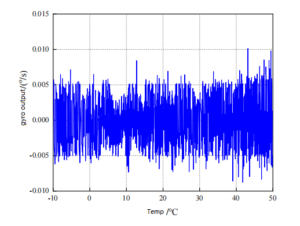
Figure 4 Piecewise fitting compensation results
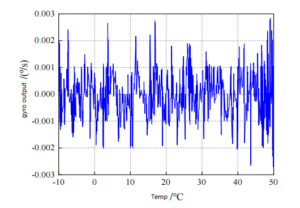
Figure 5 Compensation results of Markov chain model
It can be seen from the results of the above three methods to compensate the output of MEMS gyro sensor that the compensation result of Markov chain model is better than the other two. Comparison of the mean error and standard deviation of the compensation results of the three compensation models is shown in Table 2.
| Scheme | Mean value/(°/s) | Standard deviation/(°/s) |
| Polynomial fitting | 12.16×10-5 | 5.71×10-3 |
| Segmental fitting | 8.32×10-5 | 3.96×10-3 |
| Markov chain compensation | 6.99×10-5 | 3.04×10-3 |
Table 2 Comparison of the three methods after error compensation
As can be seen from Table 2, the effect of using Markov chain model to compensate temperature drift of MEMS gyros is better than the other two methods. The standard deviation of MEMS gyro output based on Markov chain model compensation is reduced by 46.8% compared with the traditional polynomial fitting compensation and 23.2% compared with the improved piecewise fitting compensation. It is proved that the temperature drift compensation model of MEMS gyro based on Markov chain is improved on the basis of the traditional scheme, and can deal with the temperature drift problem of MEMS gyro more effectively and improve the accuracy of MEMS gyro.
Conclusion
In this paper, the influence of temperature on MEMS gyro is analyzed, and the temperature characteristic model of MEMS gyro and the compensation algorithm model based on Markov chain are described in depth. The experimental results show that this new temperature compensation method can effectively improve the accuracy of MEMS gyro. For MEMS, Ericco has many years of research and development experience, compared to the market for a wide variety of tactical and consumer MEMS gyro sensors, Ericco mainly focuses on navigation MEMS gyro research. For example, the ER-MG2-50/100 and ER-MG2-300/400, which are north seeking gyroscopes and navigation gyroscopes respectively, can exert their excellent performance in their respective fields.
I hope that through this article you can understand the knowledge of MEMS, if you want to learn more, please click the related articles and links below to learn.
More Technical Questions
1.The analysis of damping in MEMS gyroscope
2.Sensitive structure analysis of MEMS gyroscope
3.System error and calibration of MEMS gyroscope
4.The impact of turntable error on MEMS gyroscope calibration
5.Comparative analysis of typical high performance MEMS gyroscopes
6.Borehole north finding: Shock vibration compensation for MEMS gyroscope
Products in Article







